$\int_{0}^{\frac{\pi}{2}} 2sin^{2m+1}\theta \,cos^{2n+1}\theta\, d\theta$
에서 $sin^{2}\theta=t$ 로 치환하여 적분하면
$dt=2sin\theta cos\theta d\theta$
가 되므로
$\int_{0}^{\frac{\pi}{2}} 2sin^{2m+1}\theta \,cos^{2n+1}\theta\, d\theta$
$=\int_{0}^{\frac{\pi}{2}}sin^{2m}\theta cos^{2n}\theta 2sin\theta cos\theta d\theta$
$=\int_{0}^{1} t^{m}(1-m)^{n} dt$
와 같이 정리된다.
이 형태로 정리된 식을 적분하자.
## 참고로 미분은 로그함수, 다항함수, 삼각함수, 지수함수 순으로, 로그함수가 가장 쉽고, 적분은 지수함수가 가장 쉽다. 이를 적용하면 효율적으로 문제를 풀 수 있다.##
$\int_{0}^{1} s^{m}(1-x)^{n} dx = [\frac{1}{m+1} x^{m+1}(1-x)^{n}]_{0}^{1} - \int_{0}^{1}-n(1-x)^{n-1} \frac{1}{m+1}x^{m+1}dx$
$=0-0+\frac{n}{m+1} \int_{0}{1}x^{m+1}(1-x)^{n-1}dx$
(이 과정을 반복하면)
$=\frac{(n)(n-1)}{(m+1)(m+2)}\int_{0}^{1} x^{m+2} (1-x)^{n-2}dx$
$=\cdot$
$=\cdot$
$=\cdot$
$=\frac{n(n-1)(n-2)\cdots 2\cdot 1}{(m+1)(m+2)\cdots (m+n)}\int_{0}^{1} x^{m+n}(1-x)^0 dx$
$=\frac{n(n-1)(n-2)\cdots 2\cdot 1}{(m+1)(m+2)\cdots (m+n)}[\frac{1}{m+n+1}x^{m+n+1}]_{0}^{1} = \frac{1}{m+n+1}$
$={n!\over (m+1)(m+2)\cdots (m+n+1)}$
$m=\frac{a}{b}$ 로 대입하면
$={n! \over \left(\frac{a}{b}+1\right)\left(\frac{a}{b}+2\right)\cdots \left(\frac{a}{b} + n+1\right)}$
$=b^{n+1}\cdot \frac{n!}{(a+1\cdot b)(a+2\cdot b)\cdots [a+(n-1)b]} \cdots $ 1번식
$=\int_0^1 x^{\frac{a}{b}} (1-x)^n dx$
$x=t^{\frac{b}{a+b}}$ 로 치환하면 $dx=\frac{b}{a+b} t^{\frac{-a}{a+b}}dt$
$=\int_0^1 t^{\frac{a}{a+b}} (1-t^{\frac{b}{a+b}})^n \cdot \frac{b}{a+b} t^{\frac{-a}{a+b}} dt$
$=\frac{b}{a+b} \int_0^1 (1-t^{\frac{b}{a+b}})^n dt$
$=\frac{b^{n+1}}{(a+b)^{n+1}} \int_0^1 (\frac{1-t^{\frac{b}{a+b}}}{\frac{b}{a+b}})^n dt \cdots$ 2번식
1번 식과 2번식에서 공통 인수를 약분하면 다음과 같이 정리된다.
${1\over(a+b)^{n+1}} \int_0^1 (\frac{1-t^{{b}\over a+b}}{{b\over a+b}})^n dt = {n!\over (a+b)(a+2b) \cdots (a+(n-1)b)}$
$\frac{b}{a+b}=k$ 라고 하면 $k\rightarrow 0$
$\lim_{k \to 0} \int_0^1 (\frac{1-t^k}{k})^n dt = n!$
$\int_0^1 (-ln t)^n dt = n! \rightarrow \int_0^1 (-ln x)^n dx = n!$
$-ln x = t$ 로 치환하면 $lnx=-t , x=e^{-t}, dx = -e^{-t} dt$
$n! = \int_0^1 (-lnx)^n dx$
$=\int_\infty^0 t^n (-e^{-t}) dt = \int_0^\infty t^n e^{-t} dt$
$z! = \int_0^\infty t^z e^{-t} dt = \mathit{\Gamma} (z+1)$
$\mathit{\Gamma}(1) = 1$
(claim)
$z\mathit{\Gamma}(z) = \mathit{\Gamma}(z+1)$
(proof)
$\mathit{\Gamma}(z+1)=\int_0^\infty t^z e^{-t} dt = [t^z (-e^{-t})]_0^\infty -\int_0^\infty zt^{z-1} (-e^{-t}) dt$
$=z\int_0^\infty t^{z-1} e^{-t} dt = z \mathit{\Gamma}(z)$
$\therefore Q.E.D.$
(claim)
$\int_0^\infty e^{-x^2} dx = {\sqrt{\pi} \over 2}$
$\rightarrow \mathit{\Gamma}({1\over 2}) = \int_0^\infty t^{-{1\over 2}} e^{-t} dt$
$x^2 =t$로 치환하면 $t^{-{1\over 2}} = x , 2xdx=dt$
(치환적분)
$\int_0^\infty {1\over x} e^{-x^2} 2xdx = 2\int_0^\infty e^{-x^2} dx = \sqrt{\pi}$
(proof)
$ \int_0^\infty e^{-x^2} dx= N$이라 하자. $\rightarrow \int_0^\infty e^{-y^2} dy = N$
$N^2=\int_0^\infty d^{-x^2} dx \int_0^\infty e^{-y^2} dy $
여기서 특이한 치환을 할 수 있다.
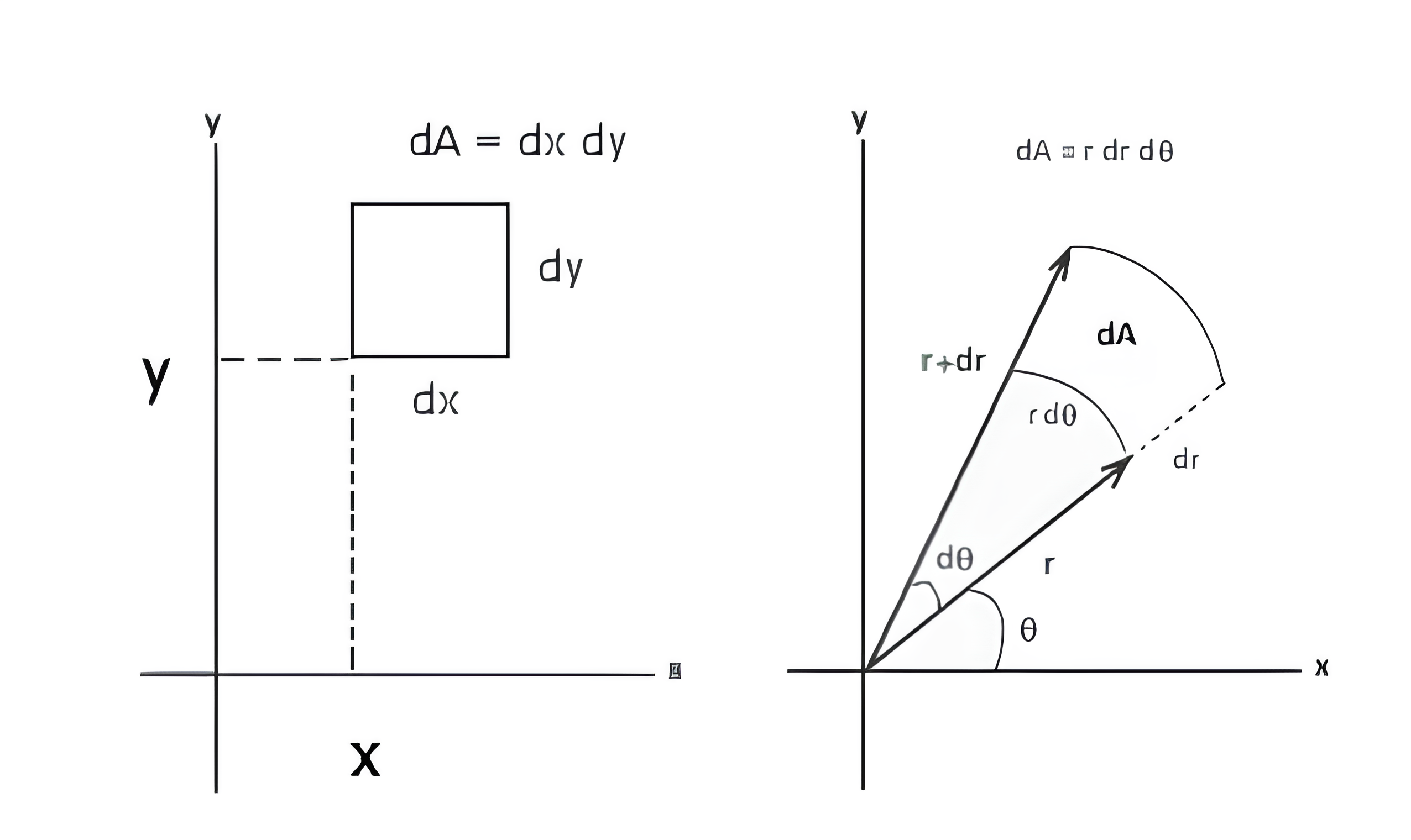
$dxdy=rdrd\theta$로 치환하자. $\rightarrow x^2+y^2=r^2$
$N^2=\int_0^\infty \int_0^\infty e^{-x^2} e^{-y^2} dxdy$
$=\int_0^{\pi \over 2} \int_0^\infty e^{-r^2} rdrd\theta$
$r^2=s$로 다시 치환하면 $2rdr=ds$
$=\int_0^{\pi\over 2}\int_0^\infty {1\over2} e^{-s} dsd\theta$
$={1\over2} \int_0^\infty e^{-s} ds \cdot \int_0^{\pi\over 2} d\theta$
$={1\over2} [-e^{-s}]_0^\infty {\pi\over2}$
$={1\over2} \cdot 1 \cdot {\pi\over2} = {\pi\over4} =N^2$
$\therefore N=\frac{\sqrt{\pi}}{2}$
$\therefore Q.E.D.$
18기 Exponential 고주원 & 19기 Exponential 전건하

댓글