대칭, 회전과 같이 '반전'이라는 것도 변환의 일종이다. 그 '반전'이라는 변환에 대해 살펴보자.
1. 반전의 정의
반지름 r인 한 원 O와 한 점 A가 주어졌을 때, $\overrightarrow{OA}$ 위의 $OA \cdot OB = r^2$ 을 만족하는 점 $B$를 원 $O$에 대한 $A$의 반전점$(inverse point)$라고 부른다. 그리고, 점집합 $X$의 각각의 점의 원 $O$에 대한 반전점들을 모은 집합 $Y$를 원 $O$에 대한 $X$의 반전이라고 부른다.
2. 원과 직선의 반전
기준원의 중심 $O$를 지나지 않는 직선의 반전은 $O$를 지나는 원이다. *기준원의 중심을 지나는 직선의 반전은 자기 자신임, 이는 자명함
<$proof$>
중심 $O$에서 그 직선에 내린 수선의 발 $M$의 반전점을 $N$이라 두고 $l$ 위의 임의의 다른 점 $X$의 반전점을 $Y$라 하자.

그렇다면, $OX \cdot OY = r^2 = OM \cdot ON$ 이므로 $\triangle OYN \backsim \triangle OMN$ 이라서 $\angle OYN = 90^\circ$ 이기 때문에 점 $Y$는 선분 $ON$을 지름으로 하는 원 위에 있다. 점 $X$를 임의의 점으로 잡았으니 다른 점들도 선분 $ON$을 지름으로 하는 원 위에 있음을 알 수 있다.
같은 방식을 반대로 하면, 반전원의 중심을 지나는 원의 반전은 직선이 됨도 알 수 있다. 그러나, 반전 기하학에서는 모든 원의 반전은 원이라고 말하는데, 이 까닭은 반전원의 중심 즉 점 $O$의 반전을 직선 양 끝의 무한 원점으로 반전된다고 생각하기 때문에 직선의 양끝이 무한 원점을 통하여 서로 연결되므로 원과 구조가 같아 이렇게 말하는 것이다.
3. 원과 원의 반전
우선, 아까 2번에서 말했다시피 원의 반전은 원이며, 기준원의 중심 $O$를 지나지 않는 원의 반전은 $O$를 지나지 않는 원이다.
<$proof$>
동심원일 때는 자명하기 때문에, 반전시키려는 원의 중심 $P$가 $O$와 다른 점이라 하자.

임의의 점 $X$의 반전점을 $X^\prime$으로 나타내기로 하자. $OX \cdot OX^\prime = OA \cdot OA^\prime = OB \cdot OB^\prime$ 이므로 $\triangle OBX \backsim \triangle OX^\prime B^\prime$, $\triangle OXA \backsim \triangle OA^\prime X^\prime$ 이라서 그림과 같이 각이 표시된다. 그런데 $\circ + \times = 90^\circ$ 이므로 $X^\prime$은 $A^\prime B^\prime$ 을 지름으로 하는 원 위의 점이다.
4. 반전과 위치 관계
서로 접하는 두 도형을 한 기준원에 대해 반전시켜도 여전히 서로 접한다. 두 집합의 교집합이 한 점이라면, 반전은 일대일대응이므로, 그 대응된 두 집합의 교집합도 한 점이기 때문이다. 이와 같은 원리로 반전이 돼도 위치관계가 변하지 않는다.
5. 구점원
포이어바흐 정리를 증명하기 전에 구점원이 무엇인지부터 알고 가자. 9개의 점을 모두 지나는 원으로, 한 삼각형의 세 변의 중점과, 세 수선의 발, 그리고 수심에서 각 꼭짓점에 이르는 세 선분의 중점까지 하여 총 9개의 점이다. 이 9개의 점이 한 원위에 있는 것은 증명된 것으로 이번 내용에서는 증명은 생략한다.
6. 포이어바흐 정리
구점원은 내접원과는 내접하고 방접원과는 외접한다는 정리이다.

그림은 다음과 같다.
7. 포이어바흐 정리 증명
<$proof$>

$B^\prime C^\prime$이 구점원의 반전임을 보이는 것이 목표이다. 4에서 본, 반전을 해도 위치관계가 변하지 않는다는 사실을 이용하는 것이다.
위 그림에서 $CY$의 길이가 파란색 접선의 길이와 같으므로 $BC$의 중점 $M$은 $XY$를 지름으로 하는 반전원의 중심이 되고 지름 $XY$의 길이는
$XY = BC - 2CY = a -2(s-b) = b-c$ 이다.
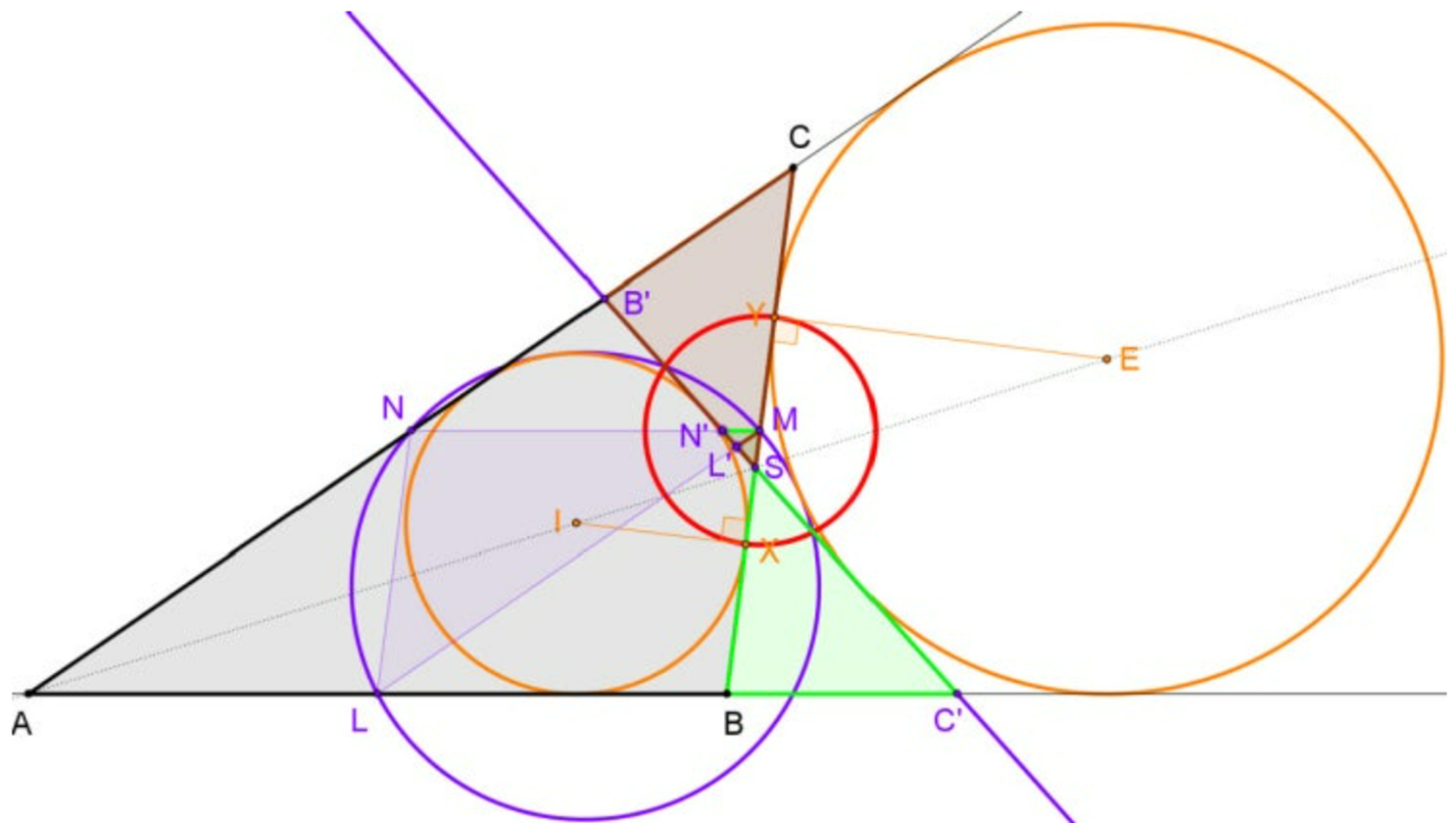
위 그림에서 $BC$와 $B^\prime C^\prime$의 교점 $S$는 $\angle A$의 이등분선 $AE$ 위의 점이므로 각의 이등분선의 정리에 의하여
$BS = BC \times \frac{AB}{AB+AC}$ $\therefore BS = \frac{ac}{b+c}$
$CS = BC \times \frac{AC}{AB+AC}$ $\therefore CS = \frac{ab}{b+c}$
또
$MS = BM - BS = \frac{a}{2} - \frac{ac}{b+c} = \frac{a(b-c)}{2(b+c)}$
$BC^\prime = AC^\prime - AB = AC - AB = b-c$
$B^\prime C = AC - AB^\prime = AC - AB = b-c$
공통 내접선 $B^\prime C^\prime$가 $MN$과 만나는 점을 $N^\prime$, $ML$과 만나는 점을 $L^\prime$라고 하면, 초록색 두 삼각형끼리 닮음이고, 갈색 두 삼각형끼리 닮음이므로,
$\triangle SBC^\prime \backsim \triangle SMN^\prime$에서
$\frac{MN^\prime}{BC^\prime} = \frac{MS}{BS}$ $\therefore \frac{MN^\prime}{b-c} = \frac{\frac{a(b-c)}{2(b+c)}}{\frac{ac}{b+c}}$
$\therefore ML^\prime = \frac{(b-c)^2}{2b}$
위의 결과를 이용하여
$MN \times MN^\prime = \frac{c}{2} \times \frac{(b-c)^2}{2c} = (\frac{b-c}{2})^2$
$ML \times ML^\prime = \frac{b}{2} \times \frac{(b-c)^2}{2b} = (\frac{b-c}{2})^2$
위 두식의 우변이 빨간색 반전원의 반지름의 제곱과 같으므로 반전의 정의를 만족한다.
$\therefore$ 구점원은 내접원과 방접원에 접한다!! $Q.E.D$
19기 EXPONENTIAL전건하 & 19기 EXPONENTIAL 유창재

댓글