
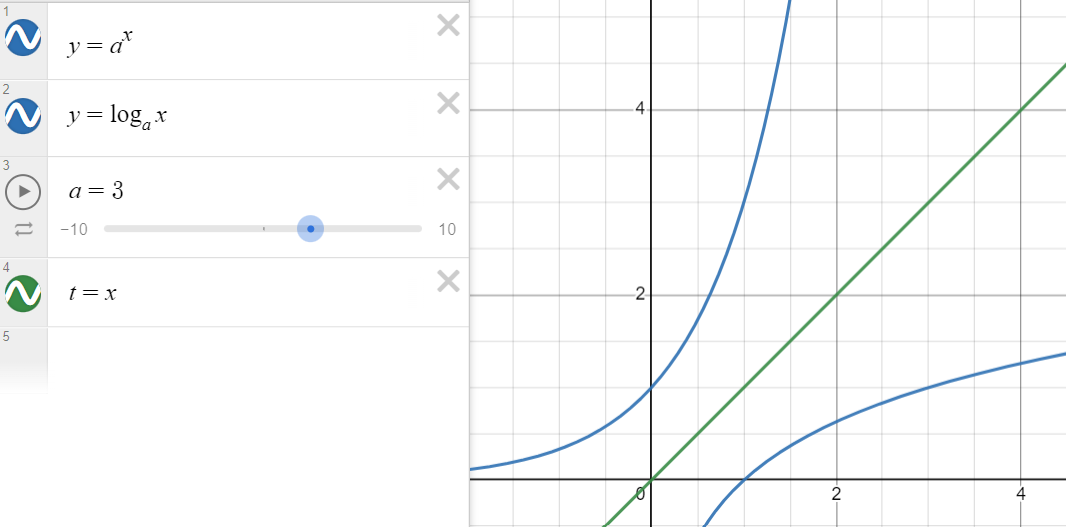
안녕하세요. 명문 학술 EXPONENTIAL의 장 17 김지하 입니다. 보통 교과서에 있는 지수함수와 그 역함수인 로그함수의 그림은 위와 같을 것입니다. 그래서 우리는 우리도 모르는 사이에 자연스레 지수함수와 역함수는 만나지 않을 것이다라는 오개념을 가지게 됩니다. 실제로는 $a$의 값에 따라 교점의 개수가 $0$부터 $3$까지 변할 수 있습니다. 이 글에서는 이 관계에 대해 살펴보고 증명할 것입니다.

1. $a>1$
우선 결론부터 말하자면
$a\in(e^{\frac{1}{e}},\infty):$ 교점 $0$개
$a=e^{\frac{1}{e}}:$ 교점 $1$개
$a\in(1,e^{\frac{1}{e}}):$ 교점 $2$개
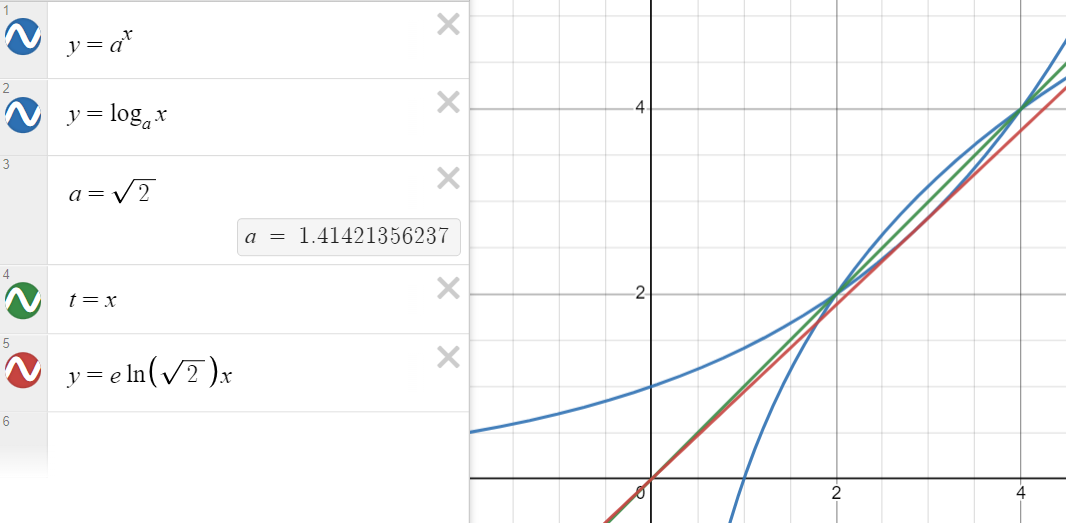
입니다. $$e^{\frac{1}{e}}\approx1.4446678$$이기 때문에 $a=\sqrt{2}$일 때는 역함수와의 교점이 $2$개 존재한다는 것을 알 수 있습니다.



먼저 사전학습을 하겠습니다.
지수함수 $y=a^x$와 접하고 원점을 지나는 접선의 방정식을 세워 봅시다. 접점의 좌표를 $(t, a^t)$라 하면 $$y=a^t\ln{a}(x-t)+a^t$$가 접선의 방정식입니다. 접선이 원점을 지나므로 $$t=\dfrac{1}{\ln{a}}=\log_{a}e$$입니다. 접선의 기울기를 구하면 $e\ln{a}$입니다.

또 증가함수와 그 역함수의 모든 교점이 $y=x$ 위에 있다는 성질을 알아야 합니다. 이로부터 증가함수와 역함수의 교점은 증가함수와 $y=x$의 교점과 같습니다. 이제 여러분들은 준비가 되었습니다.
가보자고~


접선의 기울기가 $e\ln{a}$인데 이 값이 $1$보다 크면 $x>0$에서 접선이 $y=x$보다 위에 있으므로 지수함수와 $y=x$의 교점이 없습니다. $e\ln{a}>1$을 풀면 $a>e^{\frac{1}{e}}$이므로 $a\in(e^{\frac{1}{e}},\infty)$이면 교점이 $0$개입니다.

접선의 기울기 $e\ln{a}=1$이면 지수함수와 $y=x$가 접합니다. $a=e^{\frac{1}{e}}$이면 교점이 $1$개입니다.
접선의 기울기가 $e\ln{a}$인데 이 값이 $1$보다 작으면 $x>0$에서 접선이 $y=x$보다 아래에 있으므로 지수함수와 $y=x$의 교점이 $2$개 생깁니다. $e\ln{a}<1$을 풀면 $a<e^{\frac{1}{e}}$이므로 $a\in(1,e^{\frac{1}{e}})$이면 교점이 $0$개입니다.

2. $0<a<1$
$a\in\left[\dfrac{1}{e^e},1\right):$ 교점 $1$개
$a\in\left(0,\dfrac{1}{e^e}\right):$ 교점 $3$개
입니다. 이 증명방식은 제가 생각해낸 것입니다.


사전학습을 해야합니다. 감소함수와 그 역함수의 교점이 유한개라면 한 개는 $y=x$ 위에 있고 나머지는 $y=x$에 대칭으로 두 개씩 짝을 지어 있습니다. 교점의 개수는 유한개일 때 홀수개가 됩니다.



교점이 하나뿐인 상황을 떠올려보면 두 함수의 차 $\log_a{x}-a^x$가 단조감소한다는 것을 알 수 있습니다. $$\dfrac{\operatorname{d}\!}{\operatorname{d}\!x}\left(\log_a{x}-a^x\right)=\dfrac{1}{x\ln{a}}-a^x\ln{a}=0$$의 근이 $0$개 혹은 $1$개입니다. 이 식을 가다듬으면 $$x\ln{a}\, e^{x\ln{a}}=\dfrac{1}{\ln{a}}$$가 됩니다. 이건 매우 유명한 형태죠. Lambert W function이 생각납니다. 어쨌든 우리는 이 방정식의 근의 개수를 알기 위해 $y=xe^x$의 개형을 알아야 합니다.

이 함수의 도함수는 $(x+1)e^x$고 따라서 $(-1, -e^{-1})$에서 최솟값을 가집니다. $y=x\ln{a}\, e^{x\ln{a}}$는 $x$축 방향으로 축소 또는 확대되지만 $y$축 방향으로는 그대로인 함수입니다. 그러면 $y=\dfrac{1}{\ln{a}}(<0)$과의 교점을 조사해보면 $-e^{-1}\ge\dfrac{1}{\ln{a}}$일 때 교점의 개수가 $0$개 혹은 $1$개임을 알 수 있습니다. 이 부등식을 정리하면 $\dfrac{1}{e^e}\le a<1$이 됩니다. $a\in\left[\dfrac{1}{e^e},1\right)$이면 교점이 $1$개입니다.

역함수와 교점의 개수가 유한개일 때 홀수 개이므로 교점이 $2$개인 상황은 존재하지 않습니다. 교점이 $3$개인 상황을 봅시다.

교점이 $3$개인 상황에서는 함수가 감소하다 증가하다 감소하니 $$\dfrac{\operatorname{d}\!}{\operatorname{d}\!x}\left(\log_a{x}-a^x\right)=\dfrac{1}{x\ln{a}}-a^x\ln{a}=0$$의 근이 $2$개입니다. $y=x\ln{a}\, e^{x\ln{a}}$와 $y=\dfrac{1}{\ln{a}}(<0)$과의 교점을 조사해보면 $-e^{-1}<\dfrac{1}{\ln{a}}$일 때 근이 $2$개입니다. 이 부등식을 정리하면 $0<a<\dfrac{1}{e^e}$가 됩니다. 따라서 $a\in\left(0,\dfrac{1}{e^e}\right)$이면 교점이 $3$개입니다.

여태까지 전개한 내용을 정리하겠습니다.
$a\in(e^{\frac{1}{e}},\infty):$ 교점 $0$개
$a=e^{\frac{1}{e}}:$ 교점 $1$개
$a\in(1,e^{\frac{1}{e}}):$ 교점 $2$개
$a\in\left[\dfrac{1}{e^e},1\right):$ 교점 $1$개
$a\in\left(0,\dfrac{1}{e^e}\right):$ 교점 $3$개

다음에 봬요.
'대수학' 카테고리의 다른 글
| 이항 계수의 상계와 하계 (0) | 2022.09.09 |
|---|---|
| 이항 계수 항등식 (0) | 2022.09.09 |
| 탄젠트의 배각 공식과 이항 계수 (1) | 2022.08.29 |
| 조화 급수, 오일러 급수 (0) | 2022.08.23 |
| 정십칠각형의 작도 가능성 : cos2pi/17 구하기 (1) | 2022.08.16 |

댓글