해석적 연속
해석적 연속 또는 해석적 확장이란, 복소해석학을 매게로 기존의 함수의 치역을 유지한 채 정의역을 더 넓은 범위로 확장하는 것을 말한다. 글에서 다루는 삼각함수 외에도 지수함수도 정의역을 자연수에서 정수, 유리수, 실수, 복소수로 확장해 나간다.
삼각비
정의역 : $(0,\frac{\pi}{2})$
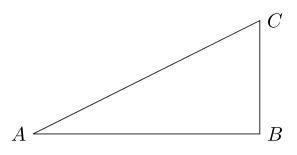
$\angle B$가 직각인 직각삼각형 $ABC$에서 삼각비들을 다음과 같이 정의한다.
$$\begin{aligned} \sin A & =\dfrac{\mathrm{AC}}{\mathrm{BC}} \\ \cos A & =\dfrac{\mathrm{AC}}{\mathrm{AB}} \\ \tan A & =\dfrac{\mathrm{AB}}{\mathrm{BC}} \\ \csc A & =\dfrac{\mathrm{BC}}{\mathrm{AC}} \\ \sec A & =\dfrac{\mathrm{AB}}{\mathrm{AC}} \\ \cot A & =\dfrac{\mathrm{BC}}{\mathrm{AB}}\end{aligned}$$
삼각함수
정의역 : $\mathbb{R}$

좌표평면 상 원점 $\rm{O}$가 중심인 단위원을 잡자. $\rm{O}$에서 시작한 $x$축의 양의 방향을 시초선, 원 위의 한 점 $\rm{P}$$(x,y)$에 대하여 $\overrightarrow{\rm{OP}}$를 동경으로 하고 반시계 방향을 양의 각이라고 하자.이때 정의되는 각의 크기를 $\theta$라고 하면, $$\begin{aligned} \sin A & =y \\ \cos A & =x \\ \tan A& =\dfrac{x}{y} \\ \csc A& =\dfrac{1}{y} \\ \sec A& =\dfrac{1}{x} \\ \cot A&=\dfrac{y}{x}\end{aligned}$$로 삼각함수를 정의한다.
복소 삼각함수
정의역 : $\mathbb{C}$
복소수 $\theta$에 대하여, $$\begin{aligned} \sin\theta & = \dfrac{e^{i\theta}-e^{-i\theta}}{2i} \\ \cos\theta & = \dfrac{e^{i\theta}+e^{-i\theta}}{2} \\ \tan \theta & = \dfrac{e^{i\theta}-e^{-i\theta}}{e^{i\theta}+e^{-i\theta}} \\ \csc\theta & = \dfrac{2}{e^{i\theta}-e^{-i\theta}} \\ \sec\theta & = \dfrac{2}{e^{i\theta}+e^{-i\theta}} \\ \cot\theta & = \dfrac{e^{i\theta}+e^{-i\theta}}{e^{i\theta}-e^{-i\theta}} \end{aligned}$$로 복소 삼각함수를 정의한다.
정의이기는 하지만, 증명은 다음과 같다.
오일러 공식 $e^{ix} =\cos x +i\sin x$에서, $x$에 $\theta$와 $-\theta$을 대입하면 다음 두 식을 얻는다.
$$\begin{aligned} e^{i\theta} & = \cos\theta +i\sin\theta \\ e^{-i\theta} & =\cos\theta-i\sin\theta\end{aligned}$$ 두 식을 더하고 빼면, $$\begin{aligned} 2\cos\theta & =e^{i\theta}+e^{-i\theta} \\ 2i\sin\theta & =e^{i\theta}-e^{-i\theta} \end{aligned}$$ 위의 식으로부터 복소 삼각함수를 정의한다.
Exponential 17 김지하
'해석학' 카테고리의 다른 글
| 연속함수 (0) | 2023.06.15 |
|---|---|
| 실수의 완비성 공리 (0) | 2023.05.21 |
| 바이어슈트라스 근사 정리 (0) | 2022.09.08 |
| 코시 수열 (0) | 2022.08.24 |

댓글