픽의 정리는 격자점의 개수를 알고싶을 때 쓰이는 강력한 정리입니다. 오일러 지표를 사용하여 픽의 정리를 증명해봅시다. (글의 이해를 위해서는 그래프 이론의 기초 내용이 필요합니다.)
우선 픽의 정리를 오일러 지표로 증명하기 위해 다음 보조정리를 증명하고 갑시다.
Lemma
임의의 꼭짓점이 모두 격자점 위에 있는 다각형을 도형 내부의 점과 변 위의 점을 통해 기본 삼각형으로 분할했을 때 생기는 변의 개수를 $e$, 처음 다각형의 내점 수를 $i$, 변 위의 점의 수를 $b$라고 하면 다음 식이 성립한다. $$e=3i+2b-3$$ (여기서 기본삼각형은 격자점을 꼭짓점으로 하는 삼각형 중에 내점이 아예 존재하지 않는 삼각형으로, 넓이는 항상 $\dfrac{1}{2}$입니다. 한 가지 혼동을 방지하자면, 기본 삼각형은 격자점 위에서 꼭짓점을 가지는 것으로 정의됩니다. 하지만 이 정리에서 나오는 점들은 그럴 필요가 전혀 없습니다.)
pf) 원래의 다각형에서 내점을 하나 더 잡는다고 하자. 그러면 위 식에서 $i$가 $+1$된 것이므로 $e$는 $3$만큼 증가할 것이다. $e$의 증가량 $3$이 불변량임을 이용하여 증명을 하자. 원래 도형에서 경계선 위에 $1$개의 점이 추가되고 $x$개의 점들이 내점으로 바뀐다고 생각하고, 변경되는 값들은 주어진 식에 대입하면 $$\begin{eqnarray} e' &&=e(i+x)+2(b-x+1)-3 \\ && = 3i+2b-3+x+2 \\ && = e+x+2 \end{eqnarray}$$이다. 여기서 $x=1$이라면 내점이 하나 늘어난 상황이므로 $e'$이 $e+3$이어야 하고, 위 식은 이를 만족하므로 증명이 완료되게 된다. $\blacksquare$
이제 이 식과 오일러 지표 $v-e+f=2$를 이용해서 픽의 정리를 증명해봅시다.
픽의 정리
모든 꼭짓점이 격자점 위에 존재하는 단순 다각형의 넓이를 $A$, 격자 다각형의 내부에 있는 점의 수를 $i$, 변 위에 있는 점의 수를 $b$라고 하면, 다음 식이 성립한다. $$A=i+\dfrac{b}{2}-1$$
증명
격자점 위에 꼭짓점이 있는 다각형을 기본 삼각형으로 분할하자.
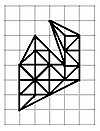
그러면, $$\begin{aligned} v & =i+b \\ e & = 3b+2b-3 \\ f & = 2i+b-1 \end{aligned}$$임은 자명하다. 오일러 지표 $$v-e+f=2$$에서 $$i+b-3i-2b+3+f=2$$이므로 따라서 $$f=2i+b-1$$ 기본 삼각형은 넓이가 $\dfrac{1}{2}$이고, 이 상황에서 $f$는 다각형의 외부까지 하나의 면으로 포함한 수이므로, $$A=\dfrac{f-1}{2}=i+\dfrac{b}{2}-1$$ 따라서 픽의 정리가 증명되었다. $\blacksquare$
Exponential 17 조인걸
'기하학' 카테고리의 다른 글
| 삼각함수의 도형으로서의 따름정리 (0) | 2023.08.28 |
|---|---|
| 원뿔곡선과 그 특별한 성질 (0) | 2023.07.25 |
| 원뿔곡선과 이차곡선 (0) | 2023.05.16 |
| 정십칠각형의 작도법 (1) | 2022.08.18 |
| 작도 가능한 수 (0) | 2022.08.16 |

댓글