이차곡선=원뿔곡선의 성질을 해석기하와 논증기하로 설명하겠다. 여기서 해석기하적 방법은 일반적으로 $y=4px^2$인 상황에서 증명한다.
기본공식) $y^2=4px$ (준선이 $x=-p$, 초점이 $(p, 0)$일 때)
1) 포물선 위의 점 $P(x_1, y_2)$에서의 접선의 방정식은 $y_1y=2p(x+x_1)$
pf) 직선을 $y=mx+n$으로 잡고 판별식과 $(x_1, y_1)$대입을 통해 구한다.
2)기울기가 m인 접선의 방정식은 $y=mx+\frac{p}{m}$
pf) $y=mx+n$으로 잡고 판별식으로 $n$을 소거하여 얻을 수 있다.
정리1) 초점이 $F$인 포물선 위의 한 점 $P$에서 준선에 내린 수선의 발을 $H$라 할 때 $P$에서의 접선은 $\angle{FPH}$를 이등분한다.
해석기하적 증명)
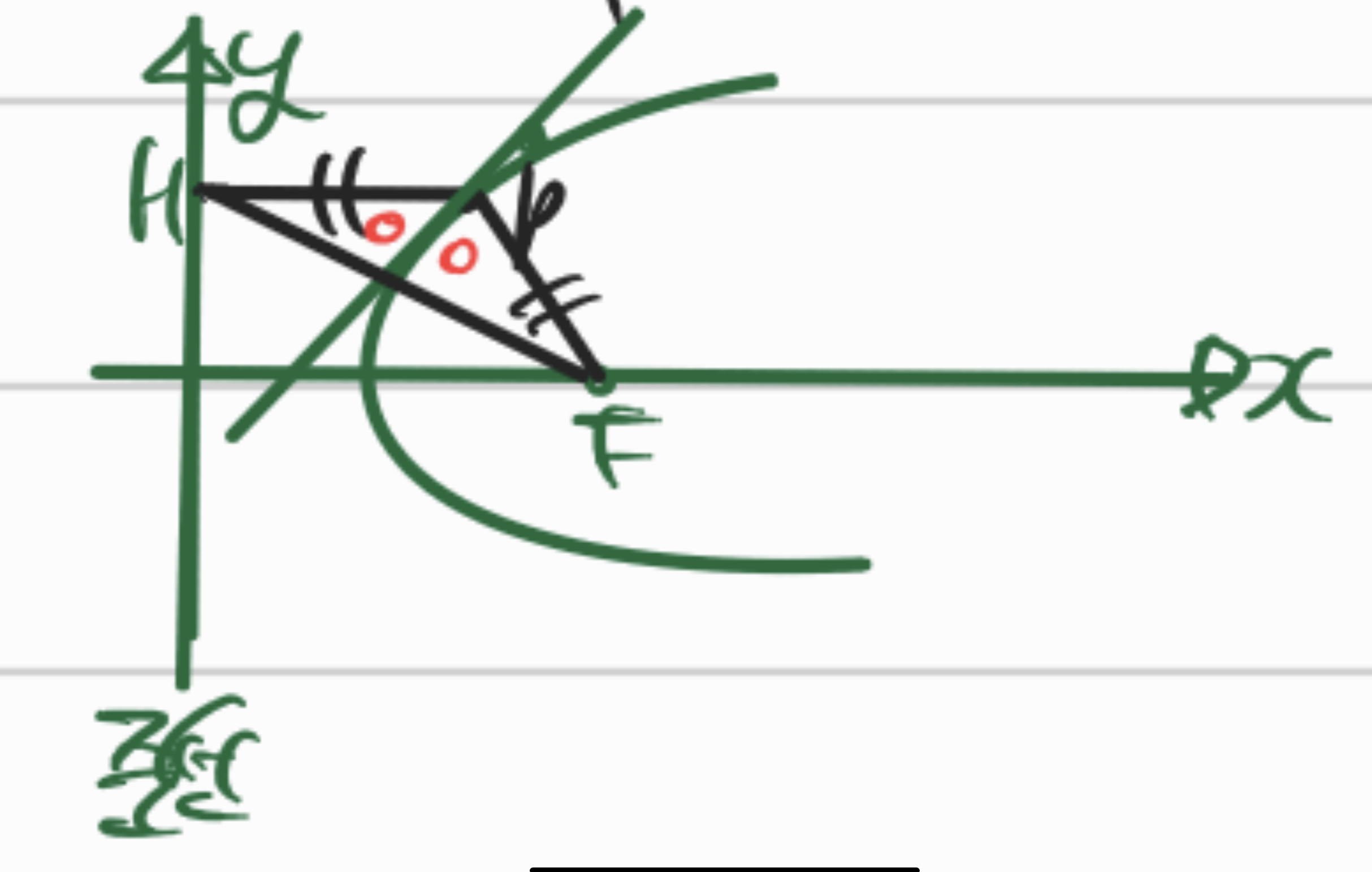
점 $P(x_1, y_1)$에서의 접선은 $y_1y=2p(x+x_1)$ 이다.
접선의 기울기는 $\frac{2p}{y_1}$ 라 할 수 있다.
여기서 점 H의 좌표는 $(-p, y_1)$이므로 $\overline{HF}$의 기울기는 $-\frac{y_1}{2p}$이다.
이 때 $P$에서의 접선이 $\overline{HF}$과 수직관계인 것을 알 수 있고 $\triangle{PHF}$가 포물선의 정의에 따라 이등변 삼각형이다.
따라서 접선이 $\angle{FPH}$를 이등분한다.
논증기하적 증명)$\angle{FPH}$의 이등분선이 $P$의 접선과 일치함을 보이면 된다.
귀류법)$\angle{FPH}$의 이등분선이 포물선과 만나는 또 다른 점 $P^\prime$이 존재한다 가정

$\angle{FPH}$의 이등분선이므로 $\triangle{P{P^\prime}H}\equiv\triangle{P{P^\prime}E}(SAS)$
이 때 $\overline{{P^\prime}F}=\overline{{P^\prime}H}$가 되고
$\overline{{P^\prime}F}=\overline{{P^\prime}H}=\overline{{P^\prime}{H^\prime}}$이 된다.
$H\ne{H^\prime}$이여서 모순이 발생하고 $H$와 $H^\prime$이 같은점이며 $P$와 $P^\prime$이 같은 점이므로 접선이 된다.
따라서 접선이 이등분한다는 것을 알 수 있다.
정리2) 포물선 위 임의의 두 점 $P$, $P^\prime$에서의 접선이 $T$에서 만난다 하자. 초점이$F$일 때 직선 $FT$가 $\angle{PFP^\prime}$을 이등분하고 ${\overline{FT}}^2={\overline{PF}}\times{\overline{{P^\prime}F}}$이다.

pf)정리1에 의해서 선분$PT$, ${P^\prime}T$는 $\overline{FH}$와 $\overline{FH^\prime}$의 수직이등분선, 두 수직이등분선의 교점이 $T$이므로 점 $T$는 $\triangle{FHH^\prime}$의 외심이다.
따라서 $\angle{HFH^\prime}=\frac{\angle{HTH^\prime}}{2}=\angle{PHT}=\angle{{P^\prime}{H^\prime}{T}}$
따라서 $\triangle{PHT}\equiv\triangle{PFT}$, $\triangle{{P^\prime}HT}\equiv\triangle{{P^\prime}FT}$
또한, $\angle{FHH^\prime}=90^\circ-\angle{PHF}=90^\circ-\angle{PFH}=\angle{FPT}$ 똑같이 하면 $\angle{F{H^\prime}H}=\angle{F{P^\prime}T}$
$\triangle{FPT}\backsim\triangle{FHH^\prime}\backsim\triangle{FTP^\prime}(AA)$
따라서 $\overline{FT}:\overline{PF}=\overline{{P^\prime}T}:\overline{{P^\prime}F}$,
$\overline{PF}\cdot\overline{{P^\prime}T}=\overline{FT}\cdot\overline{{P^\prime}F}$
이후 같은 과정을 한 번 더 반복하면
$\therefore{\overline{FT}}^2=\overline{PE}\times\overline{{P^\prime}F}$
정리3) 포물선위 임의의 점 $P$, $P^\prime$에서 그은 각각의 접선이 수직이 되는 점의 자취는 준선위에 있다.
포물선 위의 교점 $F$, 접접 $P$, $P^\prime$에서 그은 서로 수직인 접선의 교점을 T라 하자
정리 2에 의해 $\triangle{FPT}\backsim\triangle{FTP^\prime}$인데 $\angle{PTP^\prime}$가 직각이니 닮은 $\triangle{FHH^\prime}$ 또한 직각삼각형이다.
이때 $T$가 $HH^\prime$ 위에 존재하고 역으로 닮음 관계를 따지면 $\angle{PTP^\prime}=90^\circ$이다. 따라서 한점에서 포물선 에 그린 두 접선이 수직이 되는 모든 점의 자취는 준선이라 할 수 있다.
Exponential 17 이도헌 18 고주원
'기하학' 카테고리의 다른 글
| 베지어 곡선 (0) | 2023.08.31 |
|---|---|
| 삼각함수의 도형으로서의 따름정리 (0) | 2023.08.28 |
| 원뿔곡선과 이차곡선 (1) | 2023.05.16 |
| 픽의 정리 (0) | 2022.08.20 |
| 정십칠각형의 작도법 (1) | 2022.08.18 |

댓글