베지어 곡선이란 직선 위 일정한 속도로 움직일때 생기는 자취이다.
1차, 2차, 3차, ...로 점의 개수를 늘렸을 때 즉 베지어 곡선이 점 $n+1$개로 정의 될때 $n$차 베지어 곡선으로 정의 된다.
1) 1차 베지어 곡선
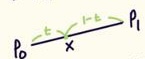
$0<t<1$일 때 $X$의 자취를 구해야 하고 $X$의 자취는 직선이라는 것을 알 수 있다.
$P_0(x_0, y_0), P_1(x_1, y_1)$라 하자.
$X$의 자취는 $P$와 $Q$를 내분한 점이므로 $X$의 $x$좌표와 $y$좌표를 $t$에 대한 방정식으로 나타낼 수 있다.
$X$의 $x$좌표 : $(1-t)x_0+tx_1$
$X$의 $y$좌표 : $(1-t)y_0+ty_1$
2) 2차 베지어 곡선

마찬가지로 $P_0(x_0, y_0), P_1(x_1, y_1), P_2(x_2, y_2)$라 하자.
1차 베지어 곡선 에서 관찰하였듯이 $x$좌표와 $y$좌표의 꼴이 유사하므로 $x$좌표에서만 확인하겠다.
$P$의 $x$좌표 : $(1-t)x_0+tx_1$
$Q$의 $y$좌표 : $(1-t)x_1+tx_2$
$X$의 $x$좌표 : $(1-t)^2x_0+t(1-t)x_1+t(1-t)x_1+t^2x_2=(1-t)^2x_0+2t(1-t)x_1+t^2x_2$
$X$의 $y$좌표 : $(1-t)^2y_0+t(1-t)y_1+t(1-t)y_1+t^2y_2=(1-t)^2y_0+2t(1-t)y_1+t^2y_2$
이때 각각의 좌표들을 원점을 시작점으로 하는 위치벡터로 나타내면 2차 베지어 곡선은 다음과 같이 나타낸다.
$B(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2(0<t<1)$($P_0, P_1, P_2$은 각각의 점에 대한 위치 벡터이다.)
3)3차 베지어 곡선
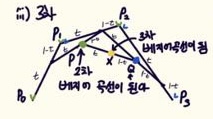
$X$의 자취가 3차 베지어 곡선이다.
또한 $P$의 자취는 $P_0, P_1, P_2$의 3차 베지어 곡선이고, $Q$의 자취는 $P_1, P_2, P_3$의 3차 베지어 곡선이다.
$P$ : $(1-t)^2P_0+2t(1-t)P_1+t^2P_2$
$Q$ : $(1-t)^2P_1+2t(1-t)P_2+t^2P_3$
$X$의 자취는 $P$와 $Q$의 내분점이다.
따라서 자취는 $(1-t)^3P_0+3t(1-t)^2P_1+3(1-t)t^2P_2+t^3P_3$이다.
4)$n$차 베지어 곡선
$P_{0123...n}$을 $P_0, P_1, P_2, ... P_n$으로 이루어진 $n$차 베지어 곡선을 만드는 자취로 정의하겠다.
3차 베지어 곡선에서도 확인할 수 있듯이 3차 베지어 곡선은 2차 베지어 곡선 2개의 1차 베지어 곡선이므로 다음과 같이 점화식으로 나타낼 수 있다.
$P_{0123...n}=tP_{0123...n-1}+(1-t)P_{123...n}$
이후 점화식을 일반화 시키면
$P_{0123...n}=\sum_{i=1}^n{n \choose i}(1-t)^{n-i}t^iP_i$
EXPONENTIAL 18TH 김은서 이주호
'기하학' 카테고리의 다른 글
| 삼각함수의 도형으로서의 따름정리 (0) | 2023.08.28 |
|---|---|
| 원뿔곡선과 그 특별한 성질 (0) | 2023.07.25 |
| 원뿔곡선과 이차곡선 (1) | 2023.05.16 |
| 픽의 정리 (0) | 2022.08.20 |
| 정십칠각형의 작도법 (1) | 2022.08.18 |

댓글